... The Programmer God ...
a Universe Simulation coded at the Planck scale


if we assign geometrical objects to mass, space and time,
and then link them via a unit number relationship, 
we can build a physical universe from mathematical structures.
Could a Programmer God have used this approach?



Articles (Nov 2025)


This is a geometrical model, Each article uses only the fine structure constant alpha, pi, an expanding universe (in integer increments) and a geometrical guide-rail. The articles 1 to 7 have been revised so that they can be read in sequential order (article 2 follows on from article 1...), and each article can be treated as a piece of the overall puzzle. The previous versions had only the original content (the model itself), so I have used AI to link to modern physics (so much quicker). This was a necessary step because this model purports to be a geometrical 'operating system' at the Planck scale, the laws of physics should therefore be able to emerge from this geometrical substrata. This is not an alternative model to physics but complementary. The laws of physics are mathematical descriptions of natural phenomena, but require postulates built in. This model should ultimately demonstrate the potential to provide the geometrical origin of these postulates. Ideally this model will also demonstrate that only 1 physical constant is required (i,.e.: being built into the source code itself), and that is the fine structure constant. In the "celestial catalogues" this would be listed as an alpha universe.

All the following articles have been compiled into a single pdf (Programmer-God_Simulation-Hypothesis_Complete-Model-2025.pdf) for AI analysis.







Philosophy


The simulation hypothesis is the proposal that all of reality, including the Earth and the rest of the universe, could be an artificial simulation, such as a computer simulation. The commonly postulated ancestor simulation approach, which Nick Bostrom called "the simulation argument", argues for "high-fidelity" simulations of ancestral life that would be indistinguishable from reality to the simulated ancestor. However this simulation variant can be traced back to an 'organic base reality' (the original programmer ancestors and their physical planet). The Programmer God hypothesis conversely states that a (deep universe) simulation began with the big bang and was programmed by an external intelligence (external to the physical universe), the Programmer by definition a God in the creator of the universe context. Our universe in its entirety, down to the smallest detail, and including life-forms, is within the simulation, the laws of nature, at their most fundamental level, are coded rules running on top of the simulation operating system. The operating system itself is mathematical (and potentially the origin of mathematics).



All articles can be seen as extensions of this article


Cite:"Programming Planck units from a virtual electron; a Simulation Hypothesis"
Eur. Phys. J. Plus (2018) 133: 278. https://doi.org/10.1140/epjp/i2018-12094-x

Planck units from a mathematical electron


top




1. Planck unit scaffolding correlates with the Cosmic Microwave Background


In this article we compare the parameters for a hypothetical Planck unit universe (sans particles) with the Cosmic Microwave Background. The model postulates a Planck unit scaffolding upon which the particle universe resides and supposes that within the CMB parameters can be found evidence of this non-baryonic background. The model uses only Planck mass and Planck length as the primary structures and a spiral geometry as the `rule set'. We begin with the peak frequency of the CMB to establish an age of the universe in Planck time units and use this as our sole variable, nevertheless from this we can derive estimates for the radiation energy density, the CMB temperature and a cold dark matter mass density that are shown to be consistent with current observational values. Intriguingly this suggests that dark matter may be predominantly non-baryonic. The Casimir force equation reduces to the equation for radiation density implying that the universe has finite boundaries, albeit these are expanding at a constant rate. This article is part of a Planck scale Simulation Hypothesis project that attempts to demonstrate that the universe could in sum total be dimensionless, relying on geometrical artifice to create actual physical structures.

Cite: "Programming relativity for use in Planck scale Simulation Hypothesis modeling".
download: doi.org/10.2139/ssrn.3333513


top




2. Relativity as the mathematics of perspective in a hyper-sphere universe


In this article we look at relativity as a translation between 2 co-ordinate systems, our relativistic 3-D space-time residing on a non-relativistic Planck unit lattice background within an expanding 4-axis hyper-sphere. The hyper-sphere expands in discrete steps (the universe is spatially finite (a closed 4-sphere), but it is not a static system, as it expands with every Planck time step), and at each step Planck units of mass m_P, length l_p and time t_p are added, thus forming a scaffolding for the particle universe. As for each unit of Planck time there is a unit of Planck length, this Planck framework is expanding at a constant rate (the speed of light c = l_p / t_p). As the hypersphere expands, it also pulls particles with it (at the speed of light), and so all particles and objects are traveling at, and only at, the speed of light (in the hyper-sphere frame of reference there is only 1 velocity, c). However, if we consider 3-D space as the surface of the hyper-sphere then motion between particles is relative. Photons are the mechanism of information exchange, as they lack a mass state they can only travel laterally across this surface (in 3-D space) and so this incremental hyper-sphere expansion at velocity $c$ cannot be observed directly via the electromagnetic spectrum, relativity then becomes the mathematics of perspective translating between the absolute albeit expanding hyper-sphere background and the relative motion of 3D space.

Cite: "2. Relativity as the mathematics of perspective in a hyper-sphere universe".
download: doi.org/10.2139/ssrn.3334282


top




3. Gravitational orbits from n-body rotating particle-particle orbital pairs


We present a geometric model of orbital mechanics in which gravitational and atomic orbits emerge from time-averaged networks of rotating point-to-point orbital pairs. The model discretizes macroscopic objects into Planck-mass points, each forming independent orbital pairs with all other points in the system, creating a universe-wide $N$-body network. Despite using only dimensionless rotating circles governed by the fine structure constant alpha and pi, the model reproduces Kepler's law and anomalous orbital precession. The simulation operates at the Planck scale, with each orbital rotating through one Planck length per Planck time (velocity c in hypersphere coordinates). Crucially, the model treats particles as oscillations between an electric wave-state (duration: particle frequency) and a mass-point state (duration: one Planck time), thereby replacing 2 abstract forces with 2 distinct states through temporal averaging. We demonstrate that when the gravitational coupling constant alpha_G is inverted, gravity becomes the dominant force at unit (Planck) time, with its apparent macroscopic weakness arising statistically from the rarity of mass-point states. The model uses only geometry, alpha, pi, and Planck units for dimensional conversion.

Cite: "3. Gravitational orbits from n-body rotating particle-particle orbital pairs".
download: doi.org/10.2139/ssrn.3444571


Gravitational and atomic orbitals
wiki: Gravitational orbital


top




4. Geometrical origins of quantization in H atom electron transitions


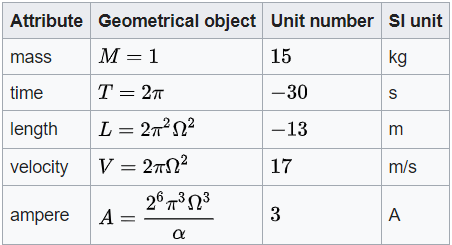
We present a geometric reformulation of Planck units and fundamental constants based on an integer-valued \emph{unit-number} map $\theta$ and a small set of dimensionless generators. Physical quantities are represented by dimensionless geometric objects constructed from $(\pi,\Omega)$ and a dimensionless fine-structure parameter $\alpha$, while \emph{local} unit systems (e.g.\ SI) enter only through two dimensioned scalars $(r,v)$ that translate the geometry into conventional units. The framework yields a unified table of constants expressible in the form $x^{\theta} i^{p} y^{q}$ with $i=\pi^{2}\Omega^{15}$, $x=\Omega v/r^{2}$, and $y=\pi r^{17}/v^{8}$, where cancellation rules enforce dimensionless invariants (units $=1$, scalars $=1$) for selected ratios. An exhaustive integer-space search over admissible unit-number assignments, subject to dimensional homogeneity, a dimensionless electron invariant $\psi$, and quark bookkeeping constraints, collapses onto a unique equivalence class characterized by the base-15 rail $3M+2T=-15$ (up to lattice shifts), selecting the canonical representative $M=15$, $T=-30$. We evaluate agreement with CODATA-2014 means using a tolerance-based coincidence model (not CODATA uncertainties) and report strong joint improbabilities for the dimensionless-combination suite, the dimensioned-constant suite, and electron-parameter reconstruction. Finally, we interpret these results through a Minimum Description Length lens: the framework acts as a compact generator that compresses many apparently independent numerical facts into a small set of structural constraints.

Cite: "4. Geometrical origins of quantization in H atom electron transitions".
download: doi.org/10.2139/ssrn.3703266


Gravitational and atomic orbitals
wiki: Gravitational orbital


top




6. Do these anomalies in the physical constants constitute evidence of coding?


We present a geometric reformulation of Planck units and fundamental constants based on an integer-valued \emph{unit-number} map $\theta$ and a small set of dimensionless generators. Physical quantities are represented by dimensionless geometric objects constructed from $(\pi,\Omega)$ and a dimensionless fine-structure parameter $\alpha$, while \emph{local} unit systems (e.g.\ SI) enter only through two dimensioned scalars $(r,v)$ that translate the geometry into conventional units. The framework yields a unified table of constants expressible in the form $x^{\theta} i^{p} y^{q}$ with $i=\pi^{2}\Omega^{15}$, $x=\Omega v/r^{2}$, and $y=\pi r^{17}/v^{8}$, where cancellation rules enforce dimensionless invariants (units $=1$, scalars $=1$) for selected ratios. An exhaustive integer-space search over admissible unit-number assignments, subject to dimensional homogeneity, a dimensionless electron invariant $\psi$, and quark bookkeeping constraints, collapses onto a unique equivalence class characterized by the base-15 rail $3M+2T=-15$ (up to lattice shifts), selecting the canonical representative $M=15$, $T=-30$. We evaluate agreement with CODATA-2014 means using a tolerance-based coincidence model (not CODATA uncertainties) and report strong joint improbabilities for the dimensionless-combination suite, the dimensioned-constant suite, and electron-parameter reconstruction. Finally, we interpret these results through a Minimum Description Length lens: the framework acts as a compact generator that compresses many apparently independent numerical facts into a small set of structural constraints.

Cite: "6. Do these anomalies in the physical constants constitute evidence of coding?".
download: doi.org/10.2139/ssrn.4346640


Physical constant anomalies
wiki: Anomalies


top




7. Geometric Origin of Quarks, the Mathematical Electron extended


Embedded within the mathematical electron formula ψ = 4\pi^2q^3 are geometrical objects with attributes of the Planck units. The object M = 1 is a unit of mass, T = pi a unit of time, P = Omega as momentum. The fine structure constant alpha and $\Omega$ (formed from pi and e) combine into a geometrical AL = q = (2^6 3 pi^2 Omega^5/alpha). This q has the units for a magnetic monopole (ampere-meter) giving the electron a q^3 internal structure that suggests quarks could be related to monopoles. We expand upon this constructing a quark model entirely from the geometrical objects; Ampere, length L and time T (themselves constructs of alpha, pi, e). We find solutions with (D = AL, charge -(1/3)e) and up (U = AV, charge +(2/3)e). The unit relationship rules between these objects permit a DDD electron but the positron would then have to be a DUU, the same configuration as the proton, which could explain the matter-antimatter asymmetry, universe neutrality and why the electron proton charge magnitudes are the same. We then investigate how a DDD configuration could have a spin-1/2.

Cite: "7. Geometric Origin of Quarks, the Mathematical Electron extended".
download: doi.org: 10.13140/RG.2.2.21695.16808


top